虚数の情緒 その２

450ページを過ぎてようやく本書の主役、虚数が登場する。ここから、ネイピア数（e）を導出して、オイラーの等式、e^iπ = -1 を導き出す。作者は、1993年に出版したオイラーの贈物でもこの等式を解説している。こちらは中学生にはやや難しく、メインは高校生以上だろう。出版当時かなり評判になった本で、僕も十数年前に読んだ。現在ハードカバーは絶版になっているが、文庫化された。
オイラーの公式を知ったのが、高校のときだったか、大学に入ってからだったか覚えていないが、この式にはぶっ飛んだなあ。

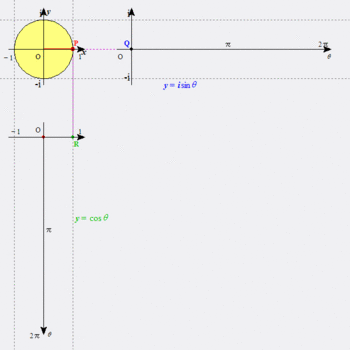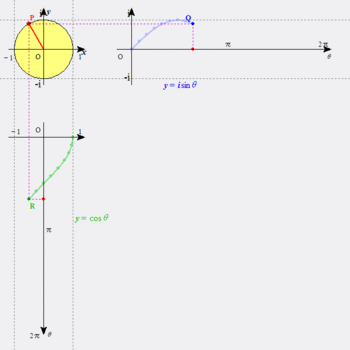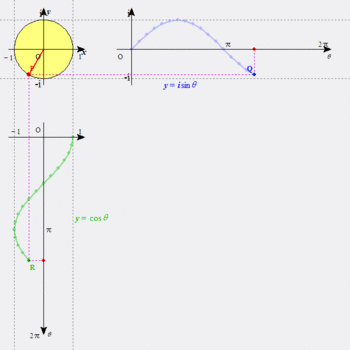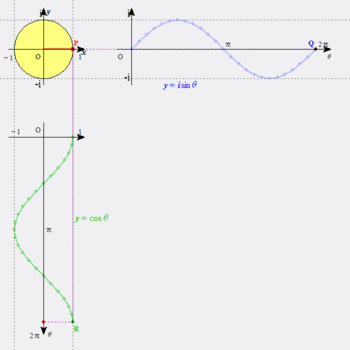
指数関数が周期関数になってるんだもの。「ホントかよ?」って感じだったなあ。図にすれば、こんな感じ。確かに両辺を等しいとしてしまえばつじつまは合うのだが、よく結び付けたもんだ。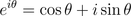

ついでだが、図のサインカーブと水平軸に囲まれた部分（0～π）の面積は2になる。これも、積分を習って計算してびっくりしたことの一つだ。整数になるとは思わなかったよ。

ネイピア数やオイラーの公式あたりの説明になると、微分・積分の考え方を使った計算がこれでもかと言うほど登場する。もう、いっそ微積分まで行ってしまった方が楽なのではないかとも思えるがそうはしない。まあ、これだけやっとけば微積分を習うときには抵抗はないだろうけど。そしてこれらの考え方が微分や積分というものだと種明かしをして、物理への応用と進む。このあたりからは読み物に戻る。

興味深かったのは、野球のバッティングの話だ。体の前へ移動を壁（軸）で止め、その運動量をバットの回転速度に加えてボールを打つ（できるのか？そんなことが）というものだ。サッカーのプレースキックに置き換えて考えてみよう。簡単のため、サッカーボールの重量を1kgとする。体重60kgの選手が秒速5mで助走して停止しているサッカーボールに弾性衝突したとする。ボールを蹴るわけではない。衝突後の選手の速度、ボールの速度をそれぞれv_a、v_bとすると次式が成り立つ。

これを解くと、v_a = 4.83 (m/s)、v_b = 9.84 (m/s)となる。ボールは時速に直すと34km/hではじきとばされることになる。これがノンステップで蹴る場合と助走をつけて蹴る場合の差で、この運動量をキックに生かせと言うわけだね。そのためにはインパクトの前、たち足を踏み込んだ時に前に移動しようする体を停止して、その運動量を蹴り足のスイング速度を増加させるように使えというのである（読み間違えてなければ）。インパクトでは、足とボールの衝突が弾性衝突に近づくよう、反発係数を上げるために足を固めることも忘れずにね。

終盤は振り子を題材に、波動関数、量子力学へと発展していく。このあたりになると、これまで丁寧に読んできたとしても、出てくる数式の理解は難しいだろう。2階の編微分方程式だもんなあ。おやじも式はきちんと追えなかったよ(T_T)
まあ、雰囲気が伝わればいいのだろうと思う。これまでの常識が思い切り覆されるので、それが面白いと感じられればいいね。そして、後半の物理部分が面白いと感じたら、もう少し大きくなって対称性を読めばいい。この本には数式は登場しないが、高校物理をやってからの方が楽しめる。

9月中旬に読み始め、1ヶ月以上かかってようやく読み終えた。子ども向けの本とは言え、1,000ページは長かったよ。